NOTE: If you’re looking for the older version please refer here.
This script takes point cloud data from the kinect, marches over the points using a marching cubes algorithm and renders a polygonal mesh. As far as I’m aware, it was the first live 3D (actual) rendering done on a kinect.
You’ll need…
Installation…
- I wrote an installation guide here, follow it to install open kinect.
- Download the latest toxiclibs library and unzip it.
- Move the unzipped toxiclibs folder into ~/Documents/Processing/libraries/
- Copy the code below and paste it in a new sketch in processing.
- Save the sketch as bubbleBoy.
- Restart processing so it knows to include the new library.
Code…
This is rather long. Basically, instead of including .java files in the sketch directory, I copied the contents into the sketch itself. Processing allows you to do this because it executes and compiles as Java anyway. All that’s needed is a minor tweak involving making marchingCubeTables a static method to allow for static fields. I also don’t include the processing.core files as you don’t need them.
NOTE: If you don’t feel like copying and pasting, I have a zip file with everything you’ll need at the bottom of this page. Just download, copy the toxiclibs library to your “libraries” folder in ~/Documents/Processing/ and copy the bubbleBoy2 directory to you “sketches” folder in ~/Documents/sketches .
import toxi.geom.Vec3D;
import processing.opengl.*;
//import rui.marchingCubes.*;
// kinect
import org.openkinect.*;
import org.openkinect.processing.*;
//import processing.core.PApplet;
import java.lang.Math;
import java.util.ArrayList;
import toxi.geom.Vec3D;
MarchingCubes mc;
Vec3D rotationAxis;
Boolean bUseFill;
// kinect
Kinect kinect;
float a = 0;
// Size of kinect image
int w = 640;
int h = 480;
int kWidth = 640;
int kHeight = 480;
// depth mapping and tilt
boolean depth = true;
boolean rgb = false;
boolean ir = false;
float deg = 8; // Start at 15 degrees
PImage depthImg;
int minDepth = 40;
int maxDepth = 860;
// set initial record to false
boolean record = false;
int counter = 0;
// print custom file
boolean printFile = false;
ArrayList points;
PrintWriter output;
// We'll use a lookup table so that we don't have to repeat the math over and over
float[] depthLookUp = new float[2048];
void setup(){
size(1024, 600, OPENGL);
Vec3D aabbMin = new Vec3D(-width/2, -height/2, -250);
Vec3D aabbMax = new Vec3D(width/2, height/2, 250);
Vec3D numPoints = new Vec3D(50,50,50);
float isoLevel = 1;
mc = new MarchingCubes(this, aabbMin, aabbMax, numPoints, isoLevel);
rotationAxis = new Vec3D();
bUseFill = false;
// kinect
kinect = new Kinect(this);
kinect.start();
kinect.enableDepth(true);
kinect.tilt(deg);
// We don't need the grayscale image in this example
// so this makes it more efficient
kinect.processDepthImage(false);
// get depthImg to constrain
depthImg = new PImage(kWidth, kHeight);
// Lookup table for all possible depth values (0 - 2047)
for (int i = 0; i < depthLookUp.length; i++) {
depthLookUp[i] = rawDepthToMeters(i);
}
points = new ArrayList();
output = createWriter("points.txt");
}
void draw(){
background(255);
lights();
// kinect
int[] depth = kinect.getRawDepth();
int skip = 50;
//translate(width/750,height/750,-50);
mc.reset();
// original for loop
println("entering loop");
int nBalls = 0;
for(int x=0; x<w; x+=skip) {
for(int y=0; y<h; y+=skip) {
int offset = x+y*w;
int rawDepth = depth[offset];
if(rawDepth >= minDepth && rawDepth <= maxDepth) {
PVector v = depthToWorld(x,y,rawDepth);
Vec3D metaBallPos = new Vec3D(v.x * 500, v.y * 300, v.z*300);
mc.addMetaBall(metaBallPos, 100, 1);
nBalls++;
}
}
}
println("done with loop, " + nBalls + " balls");
// end original for loop
mc.createMesh();
if(bUseFill){
fill(0,255,0);
noStroke();
}
else {
noFill();
stroke(127);
}
pushMatrix();
translate(width/2, height/2, 0);
rotateX(rotationAxis.x);
rotateY(rotationAxis.y);
mc.renderMesh();
popMatrix();
}
PVector depthToWorld(int x, int y, int depthValue) {
final double fx_d = 1.0 / 5.9421434211923247e+02;
final double fy_d = 1.0 / 5.9104053696870778e+02;
final double cx_d = 3.3930780975300314e+02;
final double cy_d = 2.4273913761751615e+02;
PVector result = new PVector();
double depth = depthLookUp[depthValue];//rawDepthToMeters(depthValue);
result.x = (float)((x - cx_d) * depth * fx_d);
result.y = (float)((y - cy_d) * depth * fy_d);
result.z = (float)(depth);
return result;
}
float rawDepthToMeters(int depthValue) {
if (depthValue < 2047) {
return (float)(1.0 / ((double)(depthValue) * -0.0030711016 + 3.3309495161));
}
return 0.0f;
}
void keyPressed(){
if(key == CODED){
if(keyCode == LEFT) rotationAxis.y += 0.05;
if(keyCode == RIGHT) rotationAxis.y -= 0.05;
if(keyCode == UP) rotationAxis.x -= 0.05;
if(keyCode == DOWN) rotationAxis.x += 0.05;
}
else {
if(key == ' '){
bUseFill = !bUseFill;
}
if(key == 'r' || key == 'R'){
mc.reset();
rotationAxis.set(0,0,0);
}
}
}
void stop() {
kinect.quit();
super.stop();
}
// This is because we can't find fuck all for libraries, so we'll just drop java in here as it's converted at runtime...
/**
*
*
* simple class implementing the Marching Cubes algorithm to create 3d volumetric meshes.
* based on the code and explanations by Paul Bourke that can be found here:
* http://local.wasp.uwa.edu.au/~pbourke/geometry/polygonise/
*
* its dependent on Processing's PApplet and Karsten Schmidt's Vec3D class,
* you can find processing here: www.processing.org
* and you can find the Vec3D class here: code.google.com/p/toxiclibs
*
* @author ruimadeira
*
*/
public class MarchingCubes {
PApplet p5;
public float voxelValues[][][];
protected Vec3D voxels[][][];
protected Vec3D numPoints, aabbMin, aabbMax;
protected Vec3D cubeSize;
protected Vec3D worldSize;
protected float isoLevel;
private Vec3D vertList[];
protected ArrayList<MCTriangle> triangles;
/**
* constructor:
* you must define the world bounds, the number of points that will make the grid (in a Vec3D),
* and the isoLevel.
* @param _p5
* @param _aabbMin
* @param _aabbMax
* @param _numPoints
* @param _isoLevel
*/
public MarchingCubes(PApplet _p5, Vec3D _aabbMin, Vec3D _aabbMax, Vec3D _numPoints, float _isoLevel){
p5 = _p5;
aabbMin = new Vec3D(_aabbMin);
aabbMax = new Vec3D(_aabbMax);
worldSize = aabbMax.sub(aabbMin);
numPoints = new Vec3D(_numPoints);
cubeSize = new Vec3D(worldSize.x / (numPoints.x-1), worldSize.y / (numPoints.y-1), worldSize.z / (numPoints.z-1));
voxelValues = new float[(int)numPoints.x][(int)numPoints.y][(int)numPoints.z];
voxels = new Vec3D[(int)numPoints.x][(int)numPoints.y][(int)numPoints.z];
_internalReset();
isoLevel = _isoLevel;
vertList = new Vec3D[12];
triangles = new ArrayList<MCTriangle>();
}
/**
* creates the mesh
*/
public void createMesh(){
triangles = new ArrayList<MCTriangle>();
for(int i=0; i<numPoints.x-1; i++){
for(int j=0; j<numPoints.y-1; j++){
for(int k=0; k<numPoints.z-1; k++){
polygonise(i, j, k);
}
}
}
}
/**
* returns an ArrayList of MCTriangles with all the triangles that make up the mesh
* @return
*/
public ArrayList<MCTriangle> getMesh(){
return triangles;
}
/**
* copies the mesh triangles into an array and returns
* @return
*/
public MCTriangle[] getMeshToArray(){
MCTriangle _triArray[] = new MCTriangle[triangles.size()];
triangles.toArray(_triArray);
return _triArray;
}
/**
* default rendering, renders the mesh
*/
public void renderMesh(){
MCTriangle tri;
p5.beginShape(PApplet.TRIANGLES);
for(int i=0; i<triangles.size(); i++){
tri = triangles.get(i);
p5.vertex(tri.a.x, tri.a.y, tri.a.z);
p5.vertex(tri.b.x, tri.b.y, tri.b.z);
p5.vertex(tri.c.x, tri.c.y, tri.c.z);
}
p5.endShape();
}
/**
* renders the iso grid.
* its useful for debuging.
*/
public void renderGrid(){
p5.noFill();
p5.stroke(127);
p5.beginShape(PApplet.LINES);
for(int i=0; i<numPoints.x; i++){
for(int j=0; j<numPoints.y; j++){
for(int k=0; k<numPoints.z-1; k++){
p5.vertex(voxels[i][j][k].x, voxels[i][j][k].y, voxels[i][j][k].z);
p5.vertex(voxels[i][j][k+1].x, voxels[i][j][k+1].y, voxels[i][j][k+1].z);
}
}
}
for(int i=0; i<numPoints.x; i++){
for(int j=0; j<numPoints.y-1; j++){
for(int k=0; k<numPoints.z; k++){
p5.vertex(voxels[i][j][k].x, voxels[i][j][k].y, voxels[i][j][k].z);
p5.vertex(voxels[i][j+1][k].x, voxels[i][j+1][k].y, voxels[i][j+1][k].z);
}
}
}
for(int i=0; i<numPoints.x-1; i++){
for(int j=0; j<numPoints.y; j++){
for(int k=0; k<numPoints.z; k++){
p5.vertex(voxels[i][j][k].x, voxels[i][j][k].y, voxels[i][j][k].z);
p5.vertex(voxels[i+1][j][k].x, voxels[i+1][j][k].y, voxels[i+1][j][k].z);
}
}
}
p5.endShape();
}
/**
* returns a tridimensional array of the values that each voxel has.
* you can use this to define the value of each voxel
* @return
*/
public float[][][] getValues(){
return voxelValues;
}
/**
* return the voxel grid that makes up the iso space, in a three dimensional array.
* @return
*/
public Vec3D[][][] getVoxels(){
return voxels;
}
/**
* sets the iso value of a voxel
*
* @param posX
* @param posY
* @param posZ
* @param value
*/
public void setValue(int indexX, int indexY, int indexZ, float value){
if(indexX > -1 && indexX < numPoints.x &&
indexY > -1 && indexY < numPoints.y &&
indexZ > -1 && indexZ < numPoints.z){
voxelValues[indexX][indexY][indexZ] = value;
}
}
/**
* gets the value of the specified voxel
* @param posX
* @param posY
* @param posZ
* @return
*/
public float getValue(int posX, int posY, int posZ){
if(posX > -1 && posX < numPoints.x &&
posY > -1 && posY < numPoints.y &&
posZ > -1 && posZ < numPoints.z){
return voxelValues[posX][posY][posZ];
}
return 0;
}
/**
* returns the a specific voxel of the iso space
* @param posX
* @param posY
* @param posZ
* @return
*/
public Vec3D getVoxel(int posX, int posY, int posZ){
if(posX > -1 && posX < numPoints.x &&
posY > -1 && posY < numPoints.y &&
posZ > -1 && posZ < numPoints.z){
return voxels[posX][posY][posZ];
}
return new Vec3D(0,0,0);
}
/**
* checks if the specified point is inside a voxel cube and returns the voxel.
* returns a new Vec3D if point is outside the grid.
* @param pos
* @return
*/
public Vec3D getVoxelAtWorldCoord(Vec3D point){
for(int i=0; i<voxels.length-1; i++){
for(int j=0; j<voxels[i].length-1; j++){
for(int k=0; k<voxels[i][j].length-1; k++){
if(point.x >= voxels[i][j][k].x &&
point.y >= voxels[i][j][k].y &&
point.z >= voxels[i][j][k].z &&
point.x <= voxels[i+1][j+1][k+1].x &&
point.y <= voxels[i+1][j+1][k+1].y &&
point.z <= voxels[i+1][j+1][k+1].z){
return voxels[i][j][k];
}
}
}
}
return new Vec3D();
}
/**
* adds a metaball, with the specified radius, the grid points
* inside the radius will be added the "metaValue"
* @param pos
* @param radius
* @param metaValue
*/
public void addMetaBall(Vec3D pos, float radius, float metaValue){
float radiusSQ = radius*radius;
float distSQ;
for(int i=0; i<voxels.length; i++){
for(int j=0; j<voxels[i].length; j++){
for(int k=0; k<voxels[i][j].length; k++){
distSQ = voxels[i][j][k].distanceToSquared(pos);
if(distSQ < radiusSQ){
voxelValues[i][j][k] += (1-distSQ / radiusSQ) * metaValue;
}
}
}
}
}
public void addMetaBox(Vec3D aabbMin, Vec3D aabbMax, float metaValue){
for(int i=0; i<voxels.length; i++){
for(int j=0; j<voxels[i].length; j++){
for(int k=0; k<voxels[i][j].length; k++){
if(voxels[i][j][k].x > aabbMin.x && voxels[i][j][k].y > aabbMin.y &&
voxels[i][j][k].z > aabbMin.z && voxels[i][j][k].x < aabbMax.x &&
voxels[i][j][k].y < aabbMax.y && voxels[i][j][k].z < aabbMax.z){
PApplet.println("added");
voxelValues[i][j][k] += metaValue;
}
}
}
}
}
/**
* returns the maximum voxel value
* @return
*/
public float getMax(){
float _max = voxelValues[0][0][0];
for(int i=0; i<voxels.length; i++){
for(int j=0; j<voxels[i].length; j++){
for(int k=1; k<voxels[i][j].length; k++){
if(_max < voxelValues[i][j][k])_max = voxelValues[i][j][k];
}
}
}
return _max;
}
/**
* returns the lowest voxel value
* @return
*/
public float getMin(){
float _min = voxelValues[0][0][0];
for(int i=0; i<voxels.length; i++){
for(int j=0; j<voxels[i].length; j++){
for(int k=1; k<voxels[i][j].length; k++){
if(_min > voxelValues[i][j][k])_min = voxelValues[i][j][k];
}
}
}
return _min;
}
/**
* multiplies all grid values with _val
* @param _val
*/
public void scale(float _val){
for(int i=0; i<voxels.length; i++){
for(int j=0; j<voxels[i].length; j++){
for(int k=0; k<voxels[i][j].length; k++){
voxelValues[i][j][k] *= _val;
}
}
}
}
/**
* sets all grid values with _val
* @param _val
*/
public void set(float _val){
for(int i=0; i<voxels.length; i++){
for(int j=0; j<voxels[i].length; j++){
for(int k=0; k<voxels[i][j].length; k++){
voxelValues[i][j][k] = _val;
}
}
}
}
/**
* sets the grid point with specified index with the value
* @param indexX
* @param indexY
* @param indexZ
* @param val
*/
public void set(int indexX, int indexY, int indexZ, float val){
if(indexX >-1 && indexX < numPoints.x &&
indexY >-1 && indexY < numPoints.y &&
indexZ >-1 && indexZ < numPoints.z){
voxelValues[indexX][indexY][indexZ] = val;
}
}
/**
* normalizes the voxel values
*/
public void normalize(){
float maxVal = 0;
for(int i=0; i<numPoints.x; i++){
for(int j=0; j<numPoints.y; j++){
for(int k=0; k<numPoints.z; k++){
if(voxelValues[i][j][k] > maxVal) maxVal = voxelValues[i][j][k];
}
}
}
float invertMaxVal = 1.0f/maxVal;
for(int i=0; i<numPoints.x; i++){
for(int j=0; j<numPoints.y; j++){
for(int k=0; k<numPoints.z; k++){
voxelValues[i][j][k] *= invertMaxVal;
}
}
}
}
/**
* resets the voxel values to zero
*/
public void reset(){
for(int i=0; i<numPoints.x; i++){
for(int j=0; j<numPoints.y; j++){
for(int k=0; k<numPoints.z; k++){
voxelValues[i][j][k] = 0;
}
}
}
}
/**
* redefines the minimum bounds of the iso space
* @param _aabbMin
*/
public void setAABBMin(Vec3D _aabbMin){
aabbMin.set(_aabbMin);
_internalReset();
}
/**
* returns the minimum bound of the iso space
* @return
*/
public Vec3D getAABBMin(){
return aabbMin;
}
/**
* redefines the maximum bound of the iso space
* @param _aabbMax
*/
public void setAABBMax(Vec3D _aabbMax){
aabbMax.set(_aabbMax);
_internalReset();
}
/**
* returns the maximum bound of the iso space
* @return
*/
public Vec3D getAABBMax(){
return aabbMax;
}
/**
* returns the number of triangles that make up the mesh
* @return
*/
public int getNumTriangles(){
return triangles.size();
}
/**
* returns the iso level
* @return
*/
public float getIsoLevel(){
return isoLevel;
}
/**
* sets the iso level
* @param _isoLevel
*/
public void setIsoLevel(float _isoLevel){
isoLevel = _isoLevel;
}
/**
* returns the number of vertexes that make up the iso space
* in a Vec3D: the x value represents the number of elements along the X axis,
* the y value the number of elements along the Y axis and the z value the number
* of elements along the Z axis
* @return
*/
public Vec3D getNumVoxels(){
return numPoints;
}
/**
* redefines the number of voxels that make up the grid
* @param _numPoints
*/
public void setNumVoxels(Vec3D _numPoints){
numPoints.set(_numPoints.x, _numPoints.y, _numPoints.z);
voxels = new Vec3D[(int)numPoints.x][(int)numPoints.y][(int)numPoints.z];
voxelValues = new float[(int)numPoints.x][(int)numPoints.y][(int)numPoints.z];
_internalReset();
}
/**
* returns the size of a single cube of the iso space
* @return
*/
public Vec3D getCubeSize(){
return cubeSize;
}
/**
* returns the total size of the iso space
* @return
*/
public Vec3D getWorldSize(){
return worldSize;
}
//Internals
protected void _internalReset(){
for(int i=0; i<numPoints.x; i++){
for(int j=0; j<numPoints.y; j++){
for(int k=0; k<numPoints.z; k++){
voxels[i][j][k] = new Vec3D(cubeSize.x * i, cubeSize.y * j, cubeSize.z * k);
voxels[i][j][k].x += aabbMin.x;
voxels[i][j][k].y += aabbMin.y;
voxels[i][j][k].z += aabbMin.z;
voxelValues[i][j][k] = 0;
}
}
}
}
protected void polygonise(int i, int j, int k){
int cubeIndex = 0;
if (voxelValues[i][j][k] < isoLevel) cubeIndex |= 1;
if (voxelValues[i+1][j][k] < isoLevel) cubeIndex |= 2;
if (voxelValues[i+1][j+1][k] < isoLevel) cubeIndex |= 4;
if (voxelValues[i][j+1][k] < isoLevel) cubeIndex |= 8;
if (voxelValues[i][j][k+1] < isoLevel) cubeIndex |= 16;
if (voxelValues[i+1][j][k+1] < isoLevel) cubeIndex |= 32;
if (voxelValues[i+1][j+1][k+1] < isoLevel) cubeIndex |= 64;
if (voxelValues[i][j+1][k+1] < isoLevel) cubeIndex |= 128;
/* Cube is entirely in/out of the surface */
if (MarchingCubesTables.edgeTable[cubeIndex] == 0){
return;
}
/* Find the vertices where the surface intersects the cube */
if ((MarchingCubesTables.edgeTable[cubeIndex] & 1) > 0){
vertList[0] = vertexInterp(isoLevel, voxels[i][j][k], voxels[i+1][j][k], voxelValues[i][j][k] ,voxelValues[i+1][j][k]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 2) > 0){
vertList[1] = vertexInterp(isoLevel, voxels[i+1][j][k], voxels[i+1][j+1][k], voxelValues[i+1][j][k], voxelValues[i+1][j+1][k]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 4) > 0){
vertList[2] = vertexInterp(isoLevel, voxels[i+1][j+1][k], voxels[i][j+1][k], voxelValues[i+1][j+1][k], voxelValues[i][j+1][k]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 8 ) > 0){
vertList[3] = vertexInterp(isoLevel, voxels[i][j+1][k], voxels[i][j][k], voxelValues[i][j+1][k], voxelValues[i][j][k]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 16) > 0){
vertList[4] = vertexInterp(isoLevel, voxels[i][j][k+1], voxels[i+1][j][k+1], voxelValues[i][j][k+1], voxelValues[i+1][j][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 32) > 0){
vertList[5] = vertexInterp(isoLevel, voxels[i+1][j][k+1], voxels[i+1][j+1][k+1], voxelValues[i+1][j][k+1], voxelValues[i+1][j+1][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 64) > 0){
vertList[6] = vertexInterp(isoLevel, voxels[i+1][j+1][k+1], voxels[i][j+1][k+1], voxelValues[i+1][j+1][k+1], voxelValues[i][j+1][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 128) > 0){
vertList[7] = vertexInterp(isoLevel, voxels[i][j+1][k+1], voxels[i][j][k+1], voxelValues[i][j+1][k+1], voxelValues[i][j][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 256) > 0){
vertList[8] = vertexInterp(isoLevel, voxels[i][j][k], voxels[i][j][k+1], voxelValues[i][j][k], voxelValues[i][j][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 512) > 0){
vertList[9] = vertexInterp(isoLevel, voxels[i+1][j][k], voxels[i+1][j][k+1], voxelValues[i+1][j][k], voxelValues[i+1][j][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 1024) > 0){
vertList[10] = vertexInterp(isoLevel, voxels[i+1][j+1][k], voxels[i+1][j+1][k+1], voxelValues[i+1][j+1][k], voxelValues[i+1][j+1][k+1]);
}
if ((MarchingCubesTables.edgeTable[cubeIndex] & 2048) > 0){
vertList[11] = vertexInterp(isoLevel, voxels[i][j+1][k], voxels[i][j+1][k+1], voxelValues[i][j+1][k], voxelValues[i][j+1][k+1]);
}
Vec3D vecA;
Vec3D vecB;
Vec3D normalVec = new Vec3D();
for(i=0; MarchingCubesTables.triTable[cubeIndex][i] != -1; i+=3){
vecA = vertList[MarchingCubesTables.triTable[cubeIndex][i+1]].sub(vertList[MarchingCubesTables.triTable[cubeIndex][i]]);
vecB = vertList[MarchingCubesTables.triTable[cubeIndex][i+2]].sub(vertList[MarchingCubesTables.triTable[cubeIndex][i+1]]);
normalVec = vecA.cross(vecB);
Vec3D triA = new Vec3D(vertList[MarchingCubesTables.triTable[cubeIndex][i]].x, vertList[MarchingCubesTables.triTable[cubeIndex][i]].y, vertList[MarchingCubesTables.triTable[cubeIndex][i]].z);
Vec3D triB = new Vec3D(vertList[MarchingCubesTables.triTable[cubeIndex][i+1]].x, vertList[MarchingCubesTables.triTable[cubeIndex][i+1]].y, vertList[MarchingCubesTables.triTable[cubeIndex][i+1]].z);
Vec3D triC = new Vec3D(vertList[MarchingCubesTables.triTable[cubeIndex][i+2]].x, vertList[MarchingCubesTables.triTable[cubeIndex][i+2]].y, vertList[MarchingCubesTables.triTable[cubeIndex][i+2]].z);
triangles.add(new MCTriangle(triA, triB, triC, normalVec));
}
}
protected Vec3D vertexInterp(float _isoLevel, Vec3D vertice, Vec3D vertice2, float valP1, float valP2){
float mu;
Vec3D p = new Vec3D();
if (Math.abs(isoLevel-valP1) < 0.00001)
return(vertice);
if (Math.abs(isoLevel-valP2) < 0.00001)
return(vertice2);
if (Math.abs(valP1-valP2) < 0.00001)
return(vertice);
mu = (isoLevel - valP1) / (valP2 - valP1);
p.x = vertice.x + mu * (vertice2.x - vertice.x);
p.y = vertice.y + mu * (vertice2.y - vertice.y);
p.z = vertice.z + mu * (vertice2.z - vertice.z);
return p;
}
}
/**
*
* tables, dont mess with these :)
* @author ruimadeira
*
*/
public static final class MarchingCubesTables {
public static final int edgeTable[] = {
0x0 , 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c,
0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
0x190, 0x99 , 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c,
0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
0x230, 0x339, 0x33 , 0x13a, 0x636, 0x73f, 0x435, 0x53c,
0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
0x3a0, 0x2a9, 0x1a3, 0xaa , 0x7a6, 0x6af, 0x5a5, 0x4ac,
0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
0x460, 0x569, 0x663, 0x76a, 0x66 , 0x16f, 0x265, 0x36c,
0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0xff , 0x3f5, 0x2fc,
0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x55 , 0x15c,
0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0xcc ,
0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc,
0xcc , 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c,
0x15c, 0x55 , 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc,
0x2fc, 0x3f5, 0xff , 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c,
0x36c, 0x265, 0x16f, 0x66 , 0x76a, 0x663, 0x569, 0x460,
0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac,
0x4ac, 0x5a5, 0x6af, 0x7a6, 0xaa , 0x1a3, 0x2a9, 0x3a0,
0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c,
0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x33 , 0x339, 0x230,
0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c,
0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x99 , 0x190,
0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c,
0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x0
};
public static final int triTable[][] = {
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 8, 3, 9, 8, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 2, 10, 0, 2, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 8, 3, 2, 10, 8, 10, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 11, 2, 8, 11, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 11, 2, 1, 9, 11, 9, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{3, 10, 1, 11, 10, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 10, 1, 0, 8, 10, 8, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{3, 9, 0, 3, 11, 9, 11, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 3, 0, 7, 3, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 1, 9, 4, 7, 1, 7, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 4, 7, 3, 0, 4, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1},
{9, 2, 10, 9, 0, 2, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{2, 10, 9, 2, 9, 7, 2, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{8, 4, 7, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 4, 7, 11, 2, 4, 2, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 1, 8, 4, 7, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{4, 7, 11, 9, 4, 11, 9, 11, 2, 9, 2, 1, -1, -1, -1, -1},
{3, 10, 1, 3, 11, 10, 7, 8, 4, -1, -1, -1, -1, -1, -1, -1},
{1, 11, 10, 1, 4, 11, 1, 0, 4, 7, 11, 4, -1, -1, -1, -1},
{4, 7, 8, 9, 0, 11, 9, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{4, 7, 11, 4, 11, 9, 9, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 5, 4, 1, 5, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 5, 4, 8, 3, 5, 3, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 1, 2, 10, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{5, 2, 10, 5, 4, 2, 4, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{2, 10, 5, 3, 2, 5, 3, 5, 4, 3, 4, 8, -1, -1, -1, -1},
{9, 5, 4, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 11, 2, 0, 8, 11, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{0, 5, 4, 0, 1, 5, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{2, 1, 5, 2, 5, 8, 2, 8, 11, 4, 8, 5, -1, -1, -1, -1},
{10, 3, 11, 10, 1, 3, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 5, 0, 8, 1, 8, 10, 1, 8, 11, 10, -1, -1, -1, -1},
{5, 4, 0, 5, 0, 11, 5, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{5, 4, 8, 5, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{9, 7, 8, 5, 7, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 3, 0, 9, 5, 3, 5, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 7, 8, 0, 1, 7, 1, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{1, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 7, 8, 9, 5, 7, 10, 1, 2, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 9, 5, 0, 5, 3, 0, 5, 7, 3, -1, -1, -1, -1},
{8, 0, 2, 8, 2, 5, 8, 5, 7, 10, 5, 2, -1, -1, -1, -1},
{2, 10, 5, 2, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{7, 9, 5, 7, 8, 9, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 7, 9, 7, 2, 9, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{2, 3, 11, 0, 1, 8, 1, 7, 8, 1, 5, 7, -1, -1, -1, -1},
{11, 2, 1, 11, 1, 7, 7, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 8, 8, 5, 7, 10, 1, 3, 10, 3, 11, -1, -1, -1, -1},
{5, 7, 0, 5, 0, 9, 7, 11, 0, 1, 0, 10, 11, 10, 0, -1},
{11, 10, 0, 11, 0, 3, 10, 5, 0, 8, 0, 7, 5, 7, 0, -1},
{11, 10, 5, 7, 11, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 1, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 8, 3, 1, 9, 8, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 5, 2, 6, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 5, 1, 2, 6, 3, 0, 8, -1, -1, -1, -1, -1, -1, -1},
{9, 6, 5, 9, 0, 6, 0, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 9, 8, 5, 8, 2, 5, 2, 6, 3, 2, 8, -1, -1, -1, -1},
{2, 3, 11, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 0, 8, 11, 2, 0, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 1, 9, 2, 9, 11, 2, 9, 8, 11, -1, -1, -1, -1},
{6, 3, 11, 6, 5, 3, 5, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 11, 0, 11, 5, 0, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{3, 11, 6, 0, 3, 6, 0, 6, 5, 0, 5, 9, -1, -1, -1, -1},
{6, 5, 9, 6, 9, 11, 11, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 3, 0, 4, 7, 3, 6, 5, 10, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 5, 10, 6, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, 1, 9, 7, 1, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{6, 1, 2, 6, 5, 1, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 5, 5, 2, 6, 3, 0, 4, 3, 4, 7, -1, -1, -1, -1},
{8, 4, 7, 9, 0, 5, 0, 6, 5, 0, 2, 6, -1, -1, -1, -1},
{7, 3, 9, 7, 9, 4, 3, 2, 9, 5, 9, 6, 2, 6, 9, -1},
{3, 11, 2, 7, 8, 4, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 4, 7, 2, 4, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{0, 1, 9, 4, 7, 8, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1},
{9, 2, 1, 9, 11, 2, 9, 4, 11, 7, 11, 4, 5, 10, 6, -1},
{8, 4, 7, 3, 11, 5, 3, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{5, 1, 11, 5, 11, 6, 1, 0, 11, 7, 11, 4, 0, 4, 11, -1},
{0, 5, 9, 0, 6, 5, 0, 3, 6, 11, 6, 3, 8, 4, 7, -1},
{6, 5, 9, 6, 9, 11, 4, 7, 9, 7, 11, 9, -1, -1, -1, -1},
{10, 4, 9, 6, 4, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 10, 6, 4, 9, 10, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1},
{10, 0, 1, 10, 6, 0, 6, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{8, 3, 1, 8, 1, 6, 8, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{1, 4, 9, 1, 2, 4, 2, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 1, 2, 9, 2, 4, 9, 2, 6, 4, -1, -1, -1, -1},
{0, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 3, 2, 8, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 4, 9, 10, 6, 4, 11, 2, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 2, 2, 8, 11, 4, 9, 10, 4, 10, 6, -1, -1, -1, -1},
{3, 11, 2, 0, 1, 6, 0, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{6, 4, 1, 6, 1, 10, 4, 8, 1, 2, 1, 11, 8, 11, 1, -1},
{9, 6, 4, 9, 3, 6, 9, 1, 3, 11, 6, 3, -1, -1, -1, -1},
{8, 11, 1, 8, 1, 0, 11, 6, 1, 9, 1, 4, 6, 4, 1, -1},
{3, 11, 6, 3, 6, 0, 0, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{6, 4, 8, 11, 6, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 10, 6, 7, 8, 10, 8, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{0, 7, 3, 0, 10, 7, 0, 9, 10, 6, 7, 10, -1, -1, -1, -1},
{10, 6, 7, 1, 10, 7, 1, 7, 8, 1, 8, 0, -1, -1, -1, -1},
{10, 6, 7, 10, 7, 1, 1, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 6, 1, 6, 8, 1, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{2, 6, 9, 2, 9, 1, 6, 7, 9, 0, 9, 3, 7, 3, 9, -1},
{7, 8, 0, 7, 0, 6, 6, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{7, 3, 2, 6, 7, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 11, 10, 6, 8, 10, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{2, 0, 7, 2, 7, 11, 0, 9, 7, 6, 7, 10, 9, 10, 7, -1},
{1, 8, 0, 1, 7, 8, 1, 10, 7, 6, 7, 10, 2, 3, 11, -1},
{11, 2, 1, 11, 1, 7, 10, 6, 1, 6, 7, 1, -1, -1, -1, -1},
{8, 9, 6, 8, 6, 7, 9, 1, 6, 11, 6, 3, 1, 3, 6, -1},
{0, 9, 1, 11, 6, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 8, 0, 7, 0, 6, 3, 11, 0, 11, 6, 0, -1, -1, -1, -1},
{7, 11, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 1, 9, 8, 3, 1, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 3, 0, 8, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{2, 9, 0, 2, 10, 9, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{6, 11, 7, 2, 10, 3, 10, 8, 3, 10, 9, 8, -1, -1, -1, -1},
{7, 2, 3, 6, 2, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 0, 8, 7, 6, 0, 6, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{2, 7, 6, 2, 3, 7, 0, 1, 9, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 2, 1, 8, 6, 1, 9, 8, 8, 7, 6, -1, -1, -1, -1},
{10, 7, 6, 10, 1, 7, 1, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 6, 1, 7, 10, 1, 8, 7, 1, 0, 8, -1, -1, -1, -1},
{0, 3, 7, 0, 7, 10, 0, 10, 9, 6, 10, 7, -1, -1, -1, -1},
{7, 6, 10, 7, 10, 8, 8, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{6, 8, 4, 11, 8, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 6, 11, 3, 0, 6, 0, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{8, 6, 11, 8, 4, 6, 9, 0, 1, -1, -1, -1, -1, -1, -1, -1},
{9, 4, 6, 9, 6, 3, 9, 3, 1, 11, 3, 6, -1, -1, -1, -1},
{6, 8, 4, 6, 11, 8, 2, 10, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 3, 0, 11, 0, 6, 11, 0, 4, 6, -1, -1, -1, -1},
{4, 11, 8, 4, 6, 11, 0, 2, 9, 2, 10, 9, -1, -1, -1, -1},
{10, 9, 3, 10, 3, 2, 9, 4, 3, 11, 3, 6, 4, 6, 3, -1},
{8, 2, 3, 8, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{0, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 2, 3, 4, 2, 4, 6, 4, 3, 8, -1, -1, -1, -1},
{1, 9, 4, 1, 4, 2, 2, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{8, 1, 3, 8, 6, 1, 8, 4, 6, 6, 10, 1, -1, -1, -1, -1},
{10, 1, 0, 10, 0, 6, 6, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{4, 6, 3, 4, 3, 8, 6, 10, 3, 0, 3, 9, 10, 9, 3, -1},
{10, 9, 4, 6, 10, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 5, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 4, 9, 5, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 0, 1, 5, 4, 0, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 6, 8, 3, 4, 3, 5, 4, 3, 1, 5, -1, -1, -1, -1},
{9, 5, 4, 10, 1, 2, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{6, 11, 7, 1, 2, 10, 0, 8, 3, 4, 9, 5, -1, -1, -1, -1},
{7, 6, 11, 5, 4, 10, 4, 2, 10, 4, 0, 2, -1, -1, -1, -1},
{3, 4, 8, 3, 5, 4, 3, 2, 5, 10, 5, 2, 11, 7, 6, -1},
{7, 2, 3, 7, 6, 2, 5, 4, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, 0, 8, 6, 0, 6, 2, 6, 8, 7, -1, -1, -1, -1},
{3, 6, 2, 3, 7, 6, 1, 5, 0, 5, 4, 0, -1, -1, -1, -1},
{6, 2, 8, 6, 8, 7, 2, 1, 8, 4, 8, 5, 1, 5, 8, -1},
{9, 5, 4, 10, 1, 6, 1, 7, 6, 1, 3, 7, -1, -1, -1, -1},
{1, 6, 10, 1, 7, 6, 1, 0, 7, 8, 7, 0, 9, 5, 4, -1},
{4, 0, 10, 4, 10, 5, 0, 3, 10, 6, 10, 7, 3, 7, 10, -1},
{7, 6, 10, 7, 10, 8, 5, 4, 10, 4, 8, 10, -1, -1, -1, -1},
{6, 9, 5, 6, 11, 9, 11, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{3, 6, 11, 0, 6, 3, 0, 5, 6, 0, 9, 5, -1, -1, -1, -1},
{0, 11, 8, 0, 5, 11, 0, 1, 5, 5, 6, 11, -1, -1, -1, -1},
{6, 11, 3, 6, 3, 5, 5, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 9, 5, 11, 9, 11, 8, 11, 5, 6, -1, -1, -1, -1},
{0, 11, 3, 0, 6, 11, 0, 9, 6, 5, 6, 9, 1, 2, 10, -1},
{11, 8, 5, 11, 5, 6, 8, 0, 5, 10, 5, 2, 0, 2, 5, -1},
{6, 11, 3, 6, 3, 5, 2, 10, 3, 10, 5, 3, -1, -1, -1, -1},
{5, 8, 9, 5, 2, 8, 5, 6, 2, 3, 8, 2, -1, -1, -1, -1},
{9, 5, 6, 9, 6, 0, 0, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{1, 5, 8, 1, 8, 0, 5, 6, 8, 3, 8, 2, 6, 2, 8, -1},
{1, 5, 6, 2, 1, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 3, 6, 1, 6, 10, 3, 8, 6, 5, 6, 9, 8, 9, 6, -1},
{10, 1, 0, 10, 0, 6, 9, 5, 0, 5, 6, 0, -1, -1, -1, -1},
{0, 3, 8, 5, 6, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 5, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 7, 5, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 11, 7, 5, 8, 3, 0, -1, -1, -1, -1, -1, -1, -1},
{5, 11, 7, 5, 10, 11, 1, 9, 0, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 5, 10, 11, 7, 9, 8, 1, 8, 3, 1, -1, -1, -1, -1},
{11, 1, 2, 11, 7, 1, 7, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 1, 2, 7, 1, 7, 5, 7, 2, 11, -1, -1, -1, -1},
{9, 7, 5, 9, 2, 7, 9, 0, 2, 2, 11, 7, -1, -1, -1, -1},
{7, 5, 2, 7, 2, 11, 5, 9, 2, 3, 2, 8, 9, 8, 2, -1},
{2, 5, 10, 2, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{8, 2, 0, 8, 5, 2, 8, 7, 5, 10, 2, 5, -1, -1, -1, -1},
{9, 0, 1, 5, 10, 3, 5, 3, 7, 3, 10, 2, -1, -1, -1, -1},
{9, 8, 2, 9, 2, 1, 8, 7, 2, 10, 2, 5, 7, 5, 2, -1},
{1, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 7, 0, 7, 1, 1, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 3, 9, 3, 5, 5, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{9, 8, 7, 5, 9, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{5, 8, 4, 5, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{5, 0, 4, 5, 11, 0, 5, 10, 11, 11, 3, 0, -1, -1, -1, -1},
{0, 1, 9, 8, 4, 10, 8, 10, 11, 10, 4, 5, -1, -1, -1, -1},
{10, 11, 4, 10, 4, 5, 11, 3, 4, 9, 4, 1, 3, 1, 4, -1},
{2, 5, 1, 2, 8, 5, 2, 11, 8, 4, 5, 8, -1, -1, -1, -1},
{0, 4, 11, 0, 11, 3, 4, 5, 11, 2, 11, 1, 5, 1, 11, -1},
{0, 2, 5, 0, 5, 9, 2, 11, 5, 4, 5, 8, 11, 8, 5, -1},
{9, 4, 5, 2, 11, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 5, 10, 3, 5, 2, 3, 4, 5, 3, 8, 4, -1, -1, -1, -1},
{5, 10, 2, 5, 2, 4, 4, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{3, 10, 2, 3, 5, 10, 3, 8, 5, 4, 5, 8, 0, 1, 9, -1},
{5, 10, 2, 5, 2, 4, 1, 9, 2, 9, 4, 2, -1, -1, -1, -1},
{8, 4, 5, 8, 5, 3, 3, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{0, 4, 5, 1, 0, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 4, 5, 8, 5, 3, 9, 0, 5, 0, 3, 5, -1, -1, -1, -1},
{9, 4, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 11, 7, 4, 9, 11, 9, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 4, 9, 7, 9, 11, 7, 9, 10, 11, -1, -1, -1, -1},
{1, 10, 11, 1, 11, 4, 1, 4, 0, 7, 4, 11, -1, -1, -1, -1},
{3, 1, 4, 3, 4, 8, 1, 10, 4, 7, 4, 11, 10, 11, 4, -1},
{4, 11, 7, 9, 11, 4, 9, 2, 11, 9, 1, 2, -1, -1, -1, -1},
{9, 7, 4, 9, 11, 7, 9, 1, 11, 2, 11, 1, 0, 8, 3, -1},
{11, 7, 4, 11, 4, 2, 2, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 4, 11, 4, 2, 8, 3, 4, 3, 2, 4, -1, -1, -1, -1},
{2, 9, 10, 2, 7, 9, 2, 3, 7, 7, 4, 9, -1, -1, -1, -1},
{9, 10, 7, 9, 7, 4, 10, 2, 7, 8, 7, 0, 2, 0, 7, -1},
{3, 7, 10, 3, 10, 2, 7, 4, 10, 1, 10, 0, 4, 0, 10, -1},
{1, 10, 2, 8, 7, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 1, 4, 1, 7, 7, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 1, 4, 1, 7, 0, 8, 1, 8, 7, 1, -1, -1, -1, -1},
{4, 0, 3, 7, 4, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 8, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 9, 3, 9, 11, 11, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 10, 0, 10, 8, 8, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{3, 1, 10, 11, 3, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 11, 1, 11, 9, 9, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 9, 3, 9, 11, 1, 2, 9, 2, 11, 9, -1, -1, -1, -1},
{0, 2, 11, 8, 0, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 2, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 8, 2, 8, 10, 10, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 10, 2, 0, 9, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 8, 2, 8, 10, 0, 1, 8, 1, 10, 8, -1, -1, -1, -1},
{1, 10, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 3, 8, 9, 1, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 9, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 3, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1}
};
}
import toxi.geom.Vec3D;
/**
* simple container for triangle vertices and normal
* @author ruimadeira
*
*/
public class MCTriangle {
public Vec3D a, b, c, normal;
MCTriangle(){
}
MCTriangle(Vec3D _a, Vec3D _b, Vec3D _c){
a = new Vec3D(_a);
b = new Vec3D(_b);
c = new Vec3D(_c);
normal = new Vec3D();
}
MCTriangle(Vec3D _a, Vec3D _b, Vec3D _c, Vec3D _norm){
a = new Vec3D(_a);
b = new Vec3D(_b);
c = new Vec3D(_c);
normal = new Vec3D(_norm);
}
}
Phew! I know, it’s a lot of code, but look how much you have to play with now!
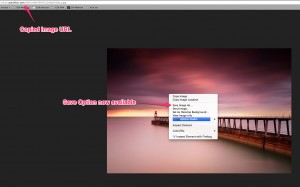
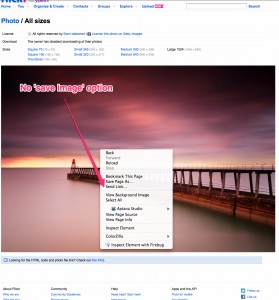 Above you can see that the common user wouldn’t be able to save this image to their desktop. However, if we inspect the element in firebug we realize the image is actually contained in a ‘div’ just a few lines above. So we can copy that image URL and save our image that way! See below…
Above you can see that the common user wouldn’t be able to save this image to their desktop. However, if we inspect the element in firebug we realize the image is actually contained in a ‘div’ just a few lines above. So we can copy that image URL and save our image that way! See below…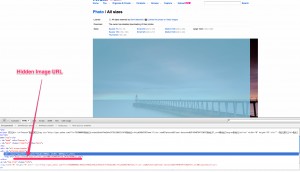 As you can see below, I copied the image url to my browser, visited the page and I can save my Image…
As you can see below, I copied the image url to my browser, visited the page and I can save my Image…